NURBS curves for shipbuilders.

Despite the fact that NURBS curves and surfaces have long been the standard tool for modeling curves and surfaces in shipbuilding, many engineers still have little idea of ​​what they are dealing with. Let's try to look at this tool not from a mathematical, but from a practical engineering point of view. Let's try to understand:

- How is NURBS different from regular splines?

- Which NURBS is better?

- What to do with the scales?

- How to determine how much of the curve will change when you move the control polygon point?

- Why don't the points of the control polygon lie on the curve?

- How is a control polygon related to a curve?

Start over.

A NURBS curve is a set of segments of parametric polynomial curves joined together (where can we get away from math?). Each NURBS point can be calculated depending on the parameter U. I think that we will not figure out what is inside Fx, Fy, Fz. Let's take this as a black box.

X = Fx (U)

Y = Fy (U)

Z = Fz (U)

As you can see from these equations, the coordinates of a point on a NURBS curve do not depend on each other and depend only on the U parameter. That is, we can draw a curve of any shape, including those with loops. This is the advantage of NURBS over traditional mathematical splines. Another advantage is the convenience of visualizing such curves. When calculating points with equal step by parameter, the curve looks smooth and beautiful. The disadvantage is that if you need to calculate a point (or points) on a curve with a fixed coordinate, you need a numerical solution. This means that the point will be calculated with the specified precision. I put your attention to this, since the aspect of accuracy is important when transferring data from one program to another.

This is also NURBS curve. So you can raw whatever you whant.

The shape of any NURBS curve is determined by the following parameters:

The degree and order of the curve.

NURBS consists of a set of polynomial segments of a given degree. The smoothness of joining the curve segments with each other, the NURBS change area when changing the position of one control point and the minimum number of possible points of the control polygon depend on the degree. The minimum possible number of control points is calculated as Degree + 1. This is called in various literature the order of the curve. You need to know this in order to meet fully armed with all kinds of CAD developers who intimidate unfortunate engineers with similar terms. Which degree is better? Probably more hight. The curve is smoother and more beautiful. Perhaps this is what we need? Below I have provided an example of NURBS degrees 1 to 5, presented on the same set of control points. See how the degree affects the shape of the curve.

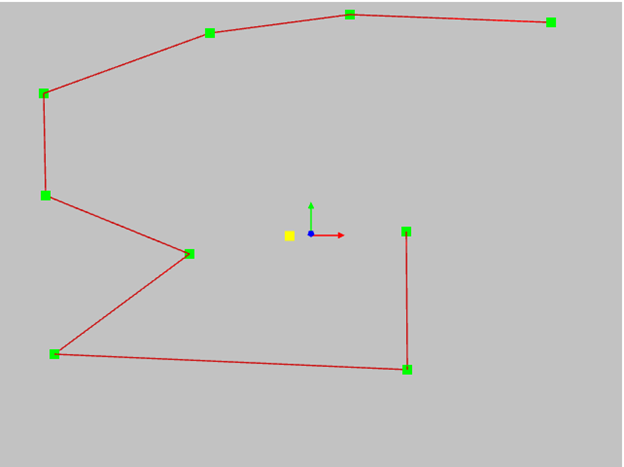
First degree - the curve matches the control polygon. Not interested. It's easier to use a polygon.

Second degree - the curve already looks like a curve.Notice an interesting property - the curve touches each line of the control polygon. It is already possible to work with such a curve, but the spans of such a curve are joined only tangentially. The curvature of such a curve changes jumps from span to span. The lack of smoothness of such a curve will be visually noticeable.

Third degree - the curve is smoother. Continuity of tangents and curvatures is performed. This degree is most commonly used in design.

Fifth degree. Better and better. Higher order derivatives are smooth. The disadvantage of these curves is that the shape of the curve is quite different from the polygon. Another disadvantage is that when you change one control point, a significant part of the curve changes. So for those who love perfectionism in designing ships, I will say - do not be surprised if, when the line changes in the area of ​​the bulb, half of the fore ship changes. This curve is much more difficult to control.

So common sense should be used when choosing a NURBS degree. As an additional argument, I will give an example of the sine or cosine function as infinitely smooth curves from the point of view of mathematics. However, no one uses them to design ships.

Control polygon.

Finally, we come to one of the most important properties of NURBS - the control polygon of the curve. As a matter of fact, this is what this class of curves and surfaces is called sculptural for. Unlike splines, where the curve passes through a set of points, the shape of NURBS curves is defined by the shape of the polygon, where the curve only passes through the start and end points of the polygon. In all other cases, the shape of the curve only repeats the shape of the polygon, but does not go through all its points. This was clearly seen in the example of changing the degree of the curve. The spline is simpler, you may say, the spline goes through all the given points. The spline is easier to manipulate. In fact, this does not play a significant role in the design, and the condition of the line passing through a given point is used very rarely. At the same time, NURBS has many more useful properties, and interactively changing the shape of a curve when changing points of a control polygon is no more difficult than changing the position of a spline point. So, the shape of the NURBS curve is determined by the shape of the control polygon. What you need to know when working with a control polygon:

- The curve starts and ends at the end points of the control polygon.

- The slope angles of the curve at the end points coincide with the slope angles of the polygon segments at the end points.

- The degree of fit of the curve at the end points depends on the length of the corresponding line segment. See picture below.

- For curves of the second degree, the curve touches each line segment

- in the case of curves of the third degree, the curve touches the polygon if three consecutive vertices lie on one straight line.In this case, the tangent point coincides with the midpoint.

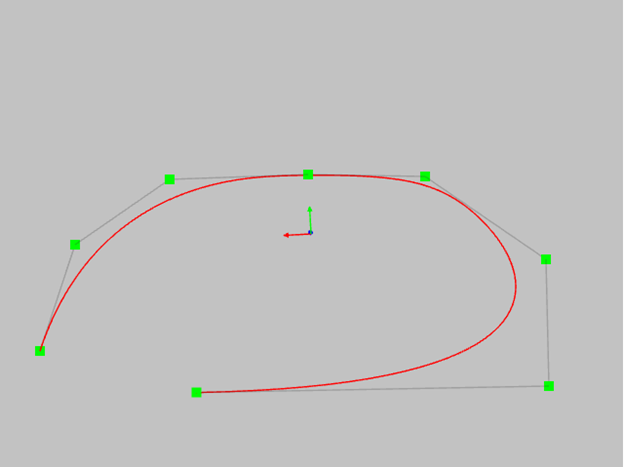
- if for a curve of the third degree four points lie on one straight line, the portion of the curve will coincide with the middle segment of the polygon and will be a mathematically exact straight line. More points on one straight line - more straight line area of our curve.

Try to do the same with a classic spline. I can say with great confidence that in this situation the classical spline will oscillate around the required straight line.

The following example shows how the fifth-degree curve behaves in this case. To get a tangent at a point, you need five points of the polygon to be on one straight line. If a strictly straight section is required, there should be even more points.In short, the higher the degree, the more difficult it is to control the shape.

- consider another, in my opinion, amazing property of NURBS curves - this is the property of the convex hull. If the polygon is convex, the curve will not have inflection points.For a non-convex polygon, the curve will always have inflections.

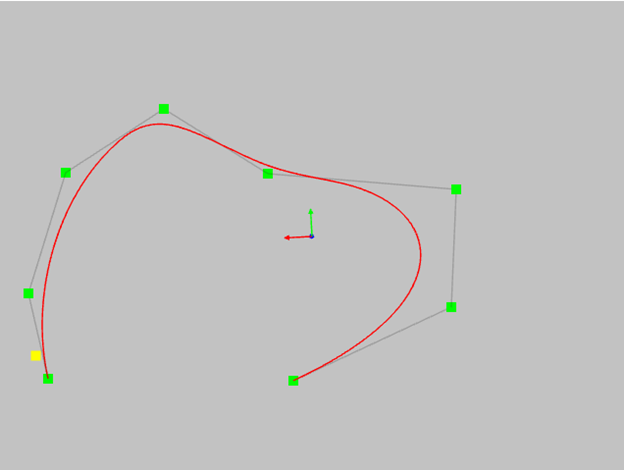
This property allows you to control the shape of the curve even without using a curvature graph.

- another very important property is the locality of the change in the shape of the curve.If you change the position of one control point, then only part of the curve will change.The range of the curve depends on the degree of NURBS.

Second degree curve.

Third degree curve.

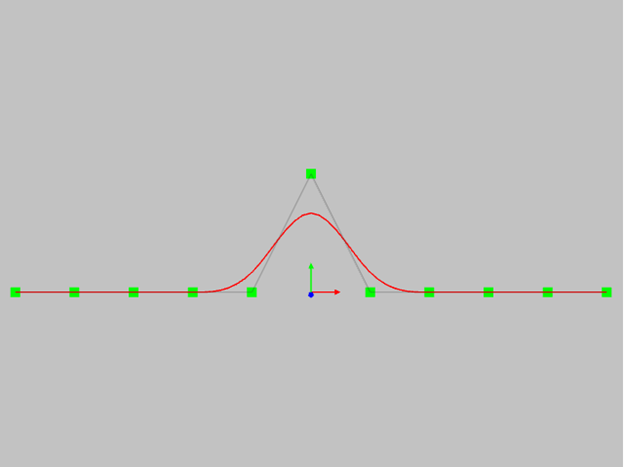
Fifth degree curve. Please note that the area of change of the curve in this case is very large.

To summarize everything we've learned here about the control polygon:

- The main tool for controlling the shape of the curve.

- Allows you to simulate a curve of almost any shape, even with straight sections.

- Allows you to locally change the shape of the curve.

- The smoothness of the curve depends on the degree of the curve, but, as elsewhere, you have to pay for everything. A high degree smooth curve is more difficult to control.

I will only add that when modeling curves, try to evenly distribute the points of the control polygon along the curve. The “pretty” control polygon defines a smooth and high quality curve.

Weight coefficients.

In the literature, as in the manuals of various 3D programs, the two terms B-Spline and NURBS are often used. What is the difference? NURBS differs from B-Spline only in that the points of the NURBS control polygon, in addition to the X, Y, Z coordinates, have an additional parameter called the weight. The meaning of this parameter is that the designer has the ability to determine which of the points of the control polygon can most strongly influence the shape of the curve. If the weights of all points are the same (which is most often the case), then this is the B-Spline. Most often, all the weight is equal to one. If the weight value at any point is equal to zero, this means that this point does not affect the shape of the curve. Mathematically beautiful, but almost incomprehensible. If a point has a weight greater than 1, for example, 2, then the curve seems to be attracted to this point. Weights are often used internally by a modeling system for highly specialized needs. For example, using weights, you can define a mathematically precise circle. This is not possible with the B-Spline. If you set the weight very high, for example 10, then the curve will run very close to the point. Visually, this may look like a knuckle point on the line. But this is only visually. The line will not match the point mathematically exactly.

This is what a curve looks like with zero weight at the center point.

All weights are 1.

Weight is 2

Weight is 10

I draw your attention to the fact that, unlike changing the degree of the curve, changing the weight at a point does not change the area of the curve modification.This is what you need to know about the weights at the points of the control polygon.

Knots vector.

A NURBS curve is a collection of polynomial curve segments. Thanks to this, we have such remarkable properties as the locality of the curve modification and the ability to straighten a part of the curve. The shape of each of these segments (also called spans) depends on several points of the control polygon. Each segment begins and ends at knot - points on the curve that represent the segment's boundaries. The knots are determined by the values ​​of the curve parameter. The number of knots is determined by the number of points of the control polygon + the order of the curve. The parametric location of the knots is determined by the knots vector. Typically, the knots vector is used for internal manipulation in 3D modeling programs. It is almost impossible to change the knots vector to change the shape of the curve. For the practical work of modeling curves, it is most important to have an even distribution of knots and segments of the curve along the parameter. In this case, the change in the position of the control points of the curve will be the most predictable.

This example shows a third degree curve with a polygon of 5 control points. In this case, the curve has two segments. The yellow dot shows the border between the segments.

The nodal vector will look like this: 0,0,0,0, 0.5,1,1,1,1 - the value 0.5 exactly corresponds to the nodal point. How are anchor points different from any other points on a curve? Anchor points help us control the shape of the curve. The example below shows the position of the node (yellow point) where the curved region of the curve begins.

Curved segments can be straight or curved only within one segment. Therefore, no matter how you want it, only at the nodal point can the curve go into a mathematically exact straight line. An example is the line of the deck turning into a flat side. I think that any shipyard will have questions to the designer if the flat side suddenly becomes a little non-flat. See picture below.

Whatever program you use to model lines and surfaces, each one uses NURBS. There can be many ways to control the shape of lines. Some programs use endpoint tangents and knots as a curve editing tool. Some allow you to modify any point on the curve. In the end, all of them still boil down to those NURBS properties that I described above. NURBS is like a musical instrument and the final result depends on the correct tuning of this instrument. The illustrations that you see in this article I made on the Internet at "nurbscalculator.in" web site. This is a simple and convenient NURBS online calculator. You can try different options for the curve parameters yourself and see how acceptable it is for you.